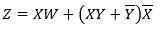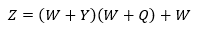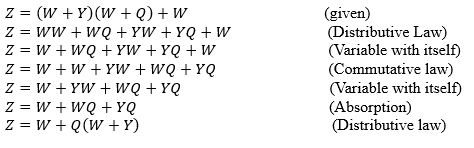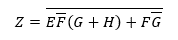Soluții la problemele capitolului 2 din baza de date online completă în domeniul informaticii și cursul de carieră pe internet de la început

Problemele și soluțiile lor

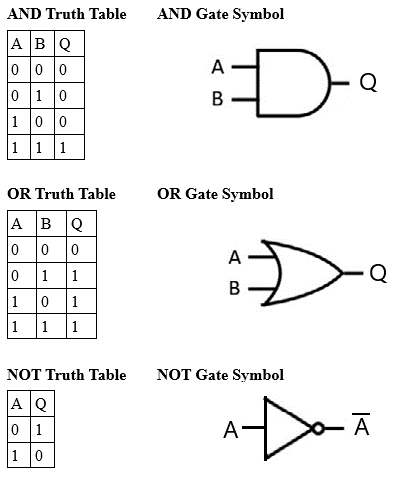
1. Produceți tabelele de adevăr ȘI, SAU și NU cu porțile corespunzătoare.

Soluţie:

2. Notează cele zece postulate booleene în diferitele lor categorii, denumind categoriile.

Funcția AND

1. 0 . 0 = 0
2. 0 . 1 = 0
3. 1 . 0 = 0
4. 1 . 1 = 1

Funcția SAU

1. 0 + 0 = 0
2. 0 + 1 = 1
3. 1 + 0 = 1
4. 1 + 1 = 1

Nu functioneaza

1. 0 = 1
2. 1 = 0

3. Fără explicații, notează cele douăzeci și șase de proprietăți ale Algebrei Booleene în diferitele lor categorii, denumind categoriile.

Proprietăți ale funcției AND

1. X . 0 = 0
2. 0 . X = 0
3. X . 1 = X
4. 1 . X = X

Proprietățile funcției SAU

1. X + 0 = X
2. 0 + X = X
3. X + 1 = 1
4. 1 + X = 1

Proprietăți pentru combinarea unei variabile cu ea însăși sau complementul acesteia

1. X . X = X
2. X.¯X = 0 la fel ca XY.¯XY = 0
3. X + X = X
4. X + X = 1

Complementare dublă

1. X ´=X

Legea comutativă

1. X. Y = Y. X
2. X + Y = Y + X

Legea distributivă

1. X(Y + Z) = XY + XZ
2. (W + X)(Y + Z) = WY + WZ + XY + XZ

Drept asociativ

1. X(YZ) = (XY)Z
2. X + (Y + Z) = (X + Y) + Z

Absorbţie

1. X + XY = X
2. X(X + Y) = X

Identitate

1. X+¯X Y =X+Y
2. X(¯X+Y) = XY

Legea lui DeMorgan

1. ¯(X+Y) = X Y
2. ¯ (X Y) =¯ X+¯Y

4. Folosind proprietățile booleene și citând categoriile utilizate, reduceți următoarea ecuație:

Soluţie:

5. Folosind proprietățile booleene și citând categoriile utilizate, reduceți următoarea ecuație:

Soluţie:

Ultimele două rânduri sunt simplificate. Cu toate acestea, este preferată ultima linie.

6. Folosind proprietățile booleene și citând categoriile utilizate, reduceți următoarea ecuație – mai întâi la suma produselor și apoi la suma minimă a produselor:

Soluţie:

Această ultimă expresie este în forma Sumă de produse (SP), dar nu în forma Sumă minimă de produse (MSP). S-a răspuns la prima parte a întrebării. Soluția pentru a doua parte este următoarea:

Această ultimă funcție (ecuație) redusă este în formă MSP.

7. Folosind proprietățile booleene și citând categoriile utilizate, reduceți următoarea ecuație – mai întâi la Suma produselor și apoi la Suma minimă a produselor:

Această ultimă ecuație (funcție) este în formă SP. Nu este o adevărată Sumă Minimă de Produse (nu este încă MSP). Deci, reducerea (minimizarea) trebuie să continue:

Această ultimă ecuație (funcție) este o adevărată Sumă Minimă de Produse (MSP).