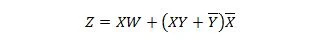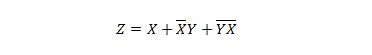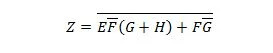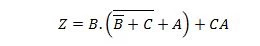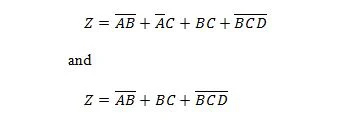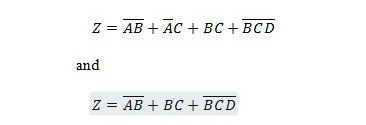Capitolul 2: Algebra booleană și componentele computerului aferente acesteia
2.1 Operatori booleeni de bază
Să presupunem că eu (autorul) sunt înalt, iar tu (cititorul) ești înalt. Dacă cineva te întreabă dacă amândoi suntem înalți, ai spune „Da” (adevărat). Dacă ne întreabă dacă amândoi suntem scunzi, ai spune „Nu” (fals). Dacă ești scund și eu sunt înalt, iar el te întreabă dacă tu sau eu suntem înalți, răspunsul tău ar fi „Da” (adevărat). Dacă ar întreabă dacă atât tu cât și eu suntem înalți, nu ai avea un răspuns. Ați putea continua spunând că ultima întrebare nu trebuie pusă sau că întrebarea nu are un răspuns. Ei bine, vreau ca tu (cititorul) să știi că astăzi, în anumite circumstanțe, întrebarea ar trebui pusă.
În biologie, o persoană este fie înaltă, fie scundă. Condițiile „de mediu” sunt cele care fac ca persoana să aibă o înălțime medie. Un om de știință, George Boole, a definit un set de răspunsuri sau reguli pentru acest tip de întrebări. Vom afla aceste reguli în această secțiune a cursului de carieră online (capitol). Aceste reguli sunt folosite astăzi în calculatoare, programare, electronică și telecomunicații. De fapt, fără aceste reguli, nu ai avea un computer, așa cum este obișnuit astăzi; nu ai avea nici programare, așa cum se întâmplă astăzi.
Adevărat sau fals
O afirmație simplă în limbajul uman este fie adevărată, fie falsă în sine. Dacă spun „Sunt înalt”, este fie adevărat, fie fals. Dacă spun „ești înalt”, este fie adevărat, fie fals. Dacă eu sunt înalt și tu ești scund și se pune întrebarea dacă atât tu cât și mine suntem înalți, în logica booleană trebuie dat un răspuns adevărat sau fals. Care dintre aceste două ar trebui să fie dat? Boole nu a răspuns cu adevărat la această întrebare. Pur și simplu a venit cu un set de reguli pe care să le respectăm. Vestea bună este că, atunci când urmați aceste reguli în contextul lor corect, nu aveți nicio ambiguitate. Datorită acestor reguli, avem calculatoare și programare astăzi. Regulile vi se dau acum. Regulile nu pot fi explicate cu adevărat; doar le accepti. Regulile sunt sub trei titluri: ȘI, SAU și NU.
ȘI
Întrebarea poate fi pusă dacă atât tu cât și eu suntem înalți. Înălțimea mea și înălțimea ta sunt apoi combinate prin setul de reguli ȘI. Acestea sunt regulile SI de urmat:
false AND false = false
false AND true = false
adevărat ȘI fals = fals
adevărat ȘI adevărat = adevărat
Acum, să fie înalt adevărat și scurt să fie fals. Asta înseamnă că dacă eu sunt scund IAR tu ești scund, tu și cu mine suntem scunzi. Daca eu sunt scunda SI tu esti inalta, tu si cu mine suntem scunzi; acesta este răspunsul boolean pe care trebuie să-l acceptați. Daca eu sunt inalt SI tu esti scund, atat tu cat si eu suntem scunzi. Dacă eu sunt înalt ȘI tu ești înalt, tu și cu mine suntem înalți. Toate acestea sunt reguli booleene SI pe care tu (cititorul) trebuie doar sa le accepti.
SAU
Întrebarea poate fi pusă dacă tu SAU eu sunt înalt. Înălțimea mea și înălțimea ta sunt apoi combinate prin setul de reguli SAU. Acestea sunt regulile SAU de urmat:
fals SAU fals = fals
fals SAU adevărat = adevărat
adevărat SAU fals = adevărat
adevărat SAU adevărat = adevărat
Din nou, să fie înalt adevărat și scurt să fie fals. Aceasta înseamnă că dacă eu sunt scund SAU tu ești scund, tu SAU eu sunt scund. Dacă eu sunt scund SAU tu ești înalt, tu sau eu suntem înalți. Dacă eu sunt înalt SAU tu ești scund, tu SAU eu sunt înalt. Dacă eu sunt înalt SAU tu ești înalt, tu sau eu suntem înalți. Toate acestea sunt reguli booleene pe care trebuie să le acceptați.
NU
Acum, în logica booleană, există doar două stări (răspunsuri posibile). Adică dacă NU ești înalt, ești scund. Daca NU esti scund, esti inalt; nimic altceva. Acestea sunt regulile NU de urmat:
NU fals = adevărat
NOT adevărat = fals
Să presupunem că aveți o sfoară (sau un arc) pe care o puteți prelungi (trage). În timp ce șirul este în starea sa naturală, dacă aș spune „NU scurt”, l-ai extinde; asta este interpretarea. În timp ce șirul este prelungit, dacă aș spune „NU lung”, i-ați permite să se contracte; asta este interpretarea.
Trebuie să memorezi toate regulile date în diferitele lor categorii.
Mai mult de doi operanzi
Într-un limbaj de calculator, AND, OR și NOT sunt fiecare numit operator. Pentru operatorul NOT, aveți nevoie de un singur operand (valoarea unui operator) pentru a avea un răspuns. Pentru operatorii AND sau OR, puteți avea mai mult de doi operanzi. Cazurile anterioare arată doi operanzi pentru AND și OR. Puteți avea trei operanzi pentru AND după cum urmează:
fals AND false AND false = fals
fals AND false AND true = fals
Acestea sunt două rânduri; fiecare are doi operatori AND. Există de fapt nouă linii când operanzii sunt trei. Cu operatorul AND, numai ultima linie (a noua linie) este egală cu adevărat; toate rândurile precedente sunt false. Rețineți că cu doi operanzi pentru AND, doar ultima linie este adevărată; toate cele trei linii precedente sunt false. Când operanzii sunt patru, există 16 linii și numai ultima linie este adevărată pentru operatorul AND.
Modelul pentru AND și modelul pentru SAU sunt diferite. Cu trei operanzi pentru doi operatori SAU, există și nouă linii și doar prima linie, de data aceasta, este falsă. Linia a doua până la a noua este adevărată. Rețineți că cu doi operanzi pentru SAU, doar prima linie este încă adevărată; toate cele trei rânduri rămase sunt false. Când operanzii sunt patru pentru OR, există și 16 linii.
Operatorul NOT se ocupă de un singur operand. NU fals este adevărat și NU adevărat este fals.
2.2 Tabelul de adevăr cu doi operanzi și componentele lor electronice
În matematică, există o temă numită algebră. O mică parte a fost văzută în capitolul anterior. Există un fel de algebră numită algebră booleană. În algebra booleană, adevăratul este identificat prin cifra de bază cu două cifre, care este 1, iar falsul este identificat prin cifra de bază două, care este 0.
Componentele unității interne ale computerului sunt componente electronice. Unitatea de sistem a sistemului informatic are componente electronice digitale. Operația AND este realizată de o mică componentă electronică numită poarta AND. Operația SAU este realizată de mica componentă electronică numită poarta SAU. Operațiunea NOT este realizată de mica componentă electronică numită poarta NOT. Prea multe dintre aceste porți pot fi într-un cip de circuit integrat (IC).
SI Tabelul Adevarului si Poarta Sa
Următorul tabel oferă tabelul de adevăr ȘI și simbolul porții ȘI (circuit mic):
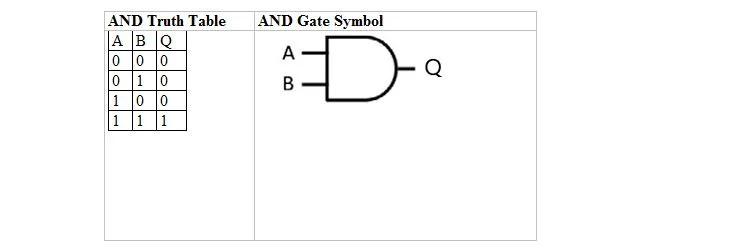
Atât pentru tabelul de adevăr AND, cât și pentru poarta sa, A și B sunt două variabile de intrare. Q este variabila de ieșire. A este fie 1, fie 0. B este fie 1, fie 0. Q este fie 1, fie 0. Tabelul de adevăr ȘI cu 1 și 0 este același cu structura anterioară adevăr/fals ȘI adevăr (tabel). Ecuația AND este:
A . B = Q
unde punctul (.) înseamnă ȘI (boolean). Punctul poate fi omis pentru a avea AB = Q, ceea ce înseamnă același lucru (ȘI).
Notă: Biții pentru A și B din cele patru rânduri, ca perechi, sunt primele patru numere din baza doi, începând de la 0 (sau 00), adică 00, 01, 10, 11.
Următorul tabel oferă tabelul de adevăr SAU și simbolul său de poartă SAU (circuit mic):
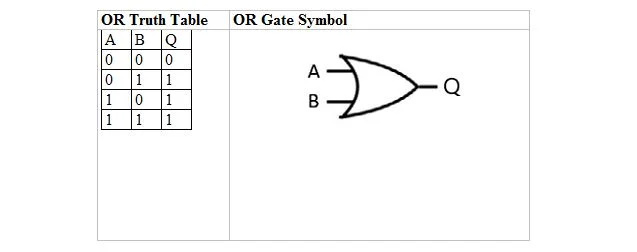
Atât pentru tabelul de adevăr SAU, cât și pentru poarta acestuia, A și B sunt două variabile de intrare. Q este variabila de ieșire. Tabelul de adevăr SAU cu 1 și 0 este același cu aspectul (tabelul) de adevăr SAU adevărat/fals anterior.
Ecuația OR este:
A + B = Q
Unde + aici înseamnă SAU boolean și nu adăugare. Ecuația se citește ca „A sau B egal cu Q”.
Următorul tabel oferă tabelul de adevăr NOT și simbolul său de poartă NOT (circuit mic):
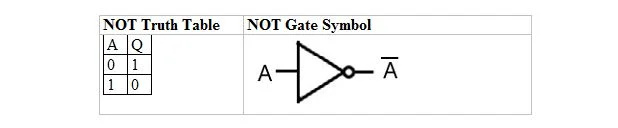
Tabelul de adevăr NOT sau poarta NOT are o singură intrare și o singură ieșire. Când intrarea este 0, ieșirea este 1. Când intrarea este 1, ieșirea este 0. Poarta NOT face un fel de inversare. Variabila de ieșire este aceeași cu variabila de intrare, dar cu o bară (supraliniată). Tabelul de adevăr NOT cu 1 și 0 este același cu aspectul anterior (tabelul) adevăr/fals SAU.
Ecuația NOT este:
A = Q
Unde Q = A și bara peste A înseamnă aici complement. Complementul lui 0 este 1, iar complementul lui 1 este 0. Poarta NOT este cunoscută și sub numele de poarta INVERSARE.
Acestea sunt tabele de adevăr fundamentale (sau rădăcină) și porțile lor (circuite mici) în electronica digitală (cu algebră booleană). Celelalte trei tabele de adevăr care sunt date în ilustrația următoare și porțile lor sunt pentru comoditate și se bazează pe cele trei tabele de adevăr anterioare.
Există o masă de adevăr și o poartă care sunt derivate din tabelul și poarta de adevăr ȘI. Ele sunt numite tabelul de adevăr NAND (pentru NOT AND) și poarta NAND corespunzătoare. Tabelul de adevăr NAND și poarta sa NAND sunt:
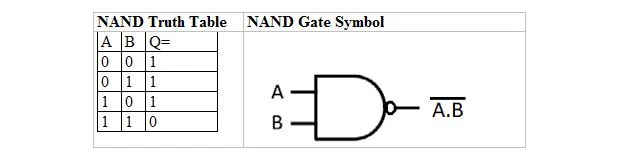
Pentru a obține tabelul de adevăr NAND, mergeți la ieșirea tabelului de adevăr AND și înlocuiți fiecare cifră cu complementul său. Complementul lui 0 este 1 și complementul lui 1 este 0. Poarta NAND este ca și poarta AND, dar are un cerc mic înaintea liniei de ieșire. Ecuația NAND este:
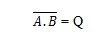
Unde înseamnă complementul rezultatului lui „A” ȘI „B”. Bara (overline) este reprezentată în poartă de cercul mic. Rețineți că punctul dintre A și B poate fi omis.
Există o altă masă de adevăr și poartă care sunt derivate din tabelul și poarta de adevăr SAU. Ele sunt numite tabelul de adevăr NOR (pentru NOT OR) și poarta NOR corespunzătoare. Tabelul de adevăr NOR și poarta sa NOR sunt:
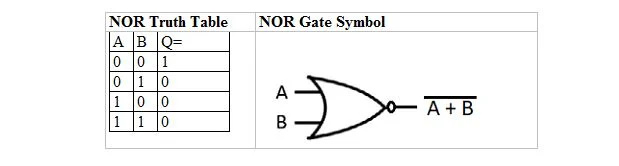
Pentru a obține tabelul de adevăr NOR, mergeți la rezultatul tabelului de adevăr OR și înlocuiți fiecare cifră cu complementul său. Complementul lui 0 este 1 și complementul lui 1 este 0. Poarta NOR este ca și poarta SAU, dar are un cerc mic înaintea liniei de ieșire. Ecuația NOR este:
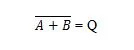
Unde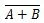 
înseamnă complementul rezultatului lui „A” SAU „B”. Bara (overline) este reprezentată în poartă de cercul mic.
SAU exclusiv (XOR)
Tabelul de adevăr pentru poarta SAU este:
În limba engleză normală, nu este clar dacă ultimul rând de 1 SAU 1 ar trebui să dea 1 sau 0. Deci, în algebra booleană, există două tipuri de tabele de adevăr SAU și două porți corespunzătoare. Cu SAU normal, ultimul rând de 1 SAU 1 dă 1. Celălalt tip de SAU este SAU exclusiv (XOR), unde primele trei rânduri sunt aceleași cu primele trei rânduri ale SAU normal (inclusiv ieșirea). Cu toate acestea, pentru al patrulea și ultimul rând, 1 SAU 1 dă 0.
Următorul tabel oferă tabelul de adevăr XOR și simbolul său de poartă XOR (circuit mic):
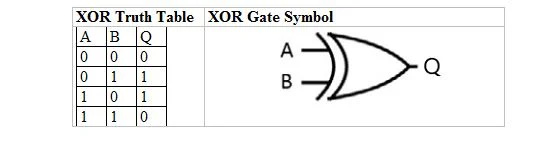
Atât pentru tabelul de adevăr XOR, cât și pentru poarta acestuia, „A”, precum și „B” sunt două variabile de intrare. „Q” este variabila de ieșire.
Ecuația XOR este:
A ⊕ B = Q
Unde ⊕ aici înseamnă XOR boolean.
SAU normal înseamnă unul sau ambele. SAU exclusiv înseamnă strict fie și nu ambele.
2.3 Postulatele booleene
Postulatele sunt ipoteze pe baza cărora se trag anumite concluzii. Există zece postulate booleene care sunt înrădăcinate din ecuațiile AND, SAU și NU (tabelele de adevăr). Aceste ecuații sunt numite și funcții. Funcțiile fundamentale sunt copiate după cum urmează:
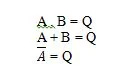
Acestea sunt funcțiile (ecuațiile) fundamentale din algebra booleană. Următoarele alte trei ecuații (funcții) nu sunt funcții fundamentale:
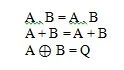
Deși ultima funcție aici este particulară, nu este considerată o funcție fundamentală.
Postulatele booleene sunt după cum urmează:
Din funcția AND
1) 0 . 0 = 0
douăzeci . 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1
Din funcția SAU
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1
Din funcția NOT
9) 0 = 1
10) 1 = 0
Notă: Aceste postulate sunt doar liniile din tabelele de adevăr ȘI, SAU și NU care sunt exprimate într-o manieră independentă. Cititorul ar trebui să memoreze postulatele date.
2.4 Proprietăți booleene
O proprietate este o caracteristică asemănătoare a ceva. Proprietățile booleene sunt ecuații care sunt derivate din postulatele booleene. În această secțiune, proprietățile sunt pur și simplu date fără derivațiile lor și apoi utilizate ulterior. Există douăzeci și cinci de proprietăți care sunt grupate în zece rubrici, după cum urmează:
Proprietăți ale funcției AND
Proprietatea 1:
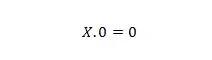
Unde X poate fi 1 sau 0. Aceasta înseamnă că indiferent de ce este X, rezultatul este întotdeauna 0.
Notă: O variabilă nu trebuie să fie neapărat A sau B sau C sau D. O variabilă poate fi W sau X sau Y sau Z sau orice altă literă.
Proprietatea 2:
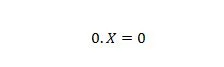
Unde X poate fi 1 sau 0. Rețineți că diferența dintre proprietatea 1 și proprietatea 2 este că în partea stângă a semnului egal al ambelor ecuații, pozițiile lui X și 0 sunt schimbate.
Proprietatea 3:
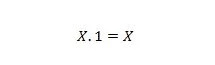
Dacă X este 0, atunci 0. 1 = 0. Dacă X este 1, atunci 1. 1 = 1.
Proprietatea 4:
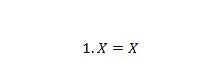
Dacă X este 0, atunci 1. 0 = 0. Dacă X este 1, atunci 1. 1 = 1. Rețineți că diferența dintre proprietatea 3 și proprietatea 4 este aceea că în partea stângă a ambelor ecuații, pozițiile lui X și 1 sunt interschimbate.
Proprietățile funcției SAU
Proprietatea 5:
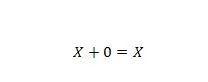
Unde X poate fi 1 sau 0. Aceasta înseamnă că dacă X este 0, rezultatul este 0. Dacă X este 1, rezultatul este 1.
Proprietatea 6:
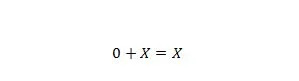
Unde X poate fi 1 sau 0. Rețineți că diferența dintre proprietatea 5 și proprietatea 6 este că în partea stângă a ambelor ecuații, pozițiile lui X și 0 sunt schimbate.
Proprietatea 7:
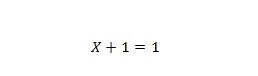
Dacă X este 0, atunci 0 + 1 = 1. Dacă X este 1, atunci 1 + 1 = 1.
Proprietatea 8:
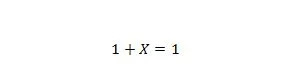
Dacă X este 0, atunci 1 + 0 = 1. Dacă X este 1, atunci 1 + 1 = 1. Rețineți că diferența dintre proprietatea 7 și proprietatea 8 este aceea că în partea stângă a ambelor ecuații, pozițiile lui X și 1 sunt interschimbate.
Proprietăți privind combinarea unei variabile cu ea însăși sau cu complementul ei
Proprietatea 9: 
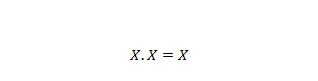
Adică: dacă X este 0, atunci 0 . 0 = 0. Dacă X este 1, atunci 1 . 1 = 1.
Proprietatea 10:
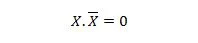
Adică: dacă X este 0, atunci 0. 1 = 0. Dacă X este 1, atunci 1. 0 = 0.
Pentru variabile consecutive, această proprietate devine:
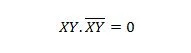
Proprietatea 11:
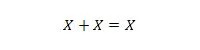
Adică: dacă X este 0, atunci 0 + 0 = 0. Dacă X este 1, atunci 1 + 1 = 1 (din OR normal).
Proprietatea 12:
Adică: dacă X este 0, atunci 0 + 1 = 1. Dacă X = 1, atunci 1 + 0 = 1.
Adică: dacă X este 0, atunci 0 + 1 = 1. Dacă X = 1, atunci 1 + 0 = 1.
Complementare dublă
Proprietatea 13:
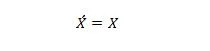
Când X pe partea stângă este 0, X pe partea dreaptă devine 0. Când X pe partea dreaptă este 1, X pe partea stângă devine 1. Cu alte cuvinte, complementele duble redau valoarea inițială.
Legea comutativă
Proprietatea 14:
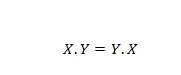
Aceasta înseamnă că interschimbarea primului și celui de-al doilea operand pentru operatorul AND, din partea stângă a semnului egal, nu contează; răspunsul rămâne același după ce a avut loc schimbul din partea stângă. Această ecuație poate fi scrisă cu punctele omise ca: XY = YX.
Proprietatea 15:
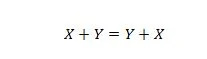
Explicația aici este aceeași ca și în precedentul AND, dar este pentru operatorul SAU.
Legea distributivă
Proprietatea 16:
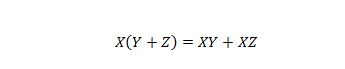
Aici există trei variabile: X, Y și Z. Fiecare variabilă poate fi fie 1, fie 0. În partea stângă a simbolului egal, parantezele înseamnă să evalueze mai întâi ceea ce este în ele. Apoi, AND este rezultatul cu X. Partea din dreapta spune că X ȘI Y împreună, SAU X ȘI Z împreună, sunt la fel cu partea stângă. Rețineți că operatorul punct pentru AND-uri este omis pe tot parcursul; iar variabilele unite înseamnă încă ŞI.
Proprietatea 17:
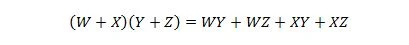
Această proprietate este o extensie a proprietății 16 cu variabila adăugată W.
Drept asociativ
Proprietatea 18:
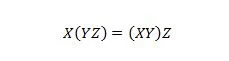
Parantezele înseamnă să evaluezi mai întâi ceea ce este în paranteze. Deci, pentru expresia din partea stângă, dacă Y cu Z sunt AND mai întâi și X este AND cu rezultatul, atunci acel rezultat final din partea stângă este același cu rezultatul final din dreapta -hand-side unde X cu Y este AND mai întâi înainte de AND a rezultat cu Z. Rețineți că punctele au fost omise în ecuație.
Proprietatea 19:
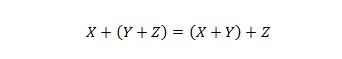
Această proprietate este explicată într-un mod similar cu proprietatea 18, dar operatorul SAU este folosit în locul operatorului AND. Operatorul SAU + nu este niciodată omis dintr-o expresie booleană de dragul simplității. Pe de altă parte, operatorul AND poate fi omis și cele două variabile pot fi unite.
Absorbţie
Proprietatea 20:
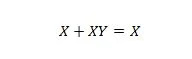
Cu această ecuație, indiferent ce este Y, partea dreaptă va fi întotdeauna X (absorbită).
Proprietatea 21:
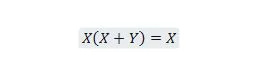
De asemenea, cu această ecuație, indiferent ce este Y, partea dreaptă va fi întotdeauna X (absorbită). Această proprietate 21 este aceeași cu proprietatea 20, care este:
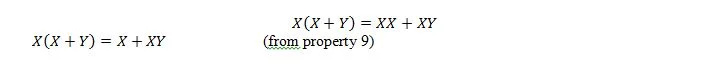
Aici, folosim legea distributivă și faptul că X.X = X a proprietății 9.
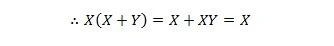
O identitate
Proprietatea 22:
Aceasta înseamnă că pentru expresia X + Y, complementul lui X în fața lui Y nu modifică expresia.
Proprietatea 23:
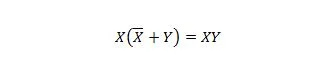
Aceasta înseamnă că pentru expresia XY, complementul lui X OR cu Y între paranteze, care se face mai întâi, nu schimbă expresia XY.
Legea lui DeMorgan
Proprietatea 24:
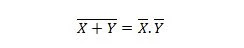
Aceasta înseamnă că o poartă NOR (NOT OR) are același rezultat ca NOTING cele două intrări înainte de AND-le.
Proprietatea 25:
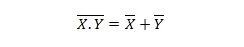
Aceasta înseamnă că o poartă NAND (NU ȘI) are același rezultat ca și notarea celor două intrări înainte de OR.
Ilustrațiile furnizate sunt cele 25 de proprietăți. Ele pot fi dovedite prin înlocuirea tuturor diferitelor valori posibile ale lui 1 și 0, în fiecare expresie din partea stângă, pentru a vedea dacă se obține expresia (sau rezultatul) din partea dreaptă. Dovezile sunt lăsate ca un exercițiu pentru cititor.
2.5 Simplificarea expresiilor compuse
Următoarele două funcții sunt aceleași:
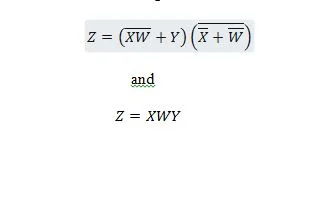
Z este ieșirea și X, W și Y sunt intrările. Primul are nevoie de o poartă NAND, o poartă OR, o poartă AND, două porți NOT, o poartă OR și o poartă NOR. Al doilea are nevoie de doar două porți AND. Prima este o ecuație cu o expresie compusă, în partea dreaptă, care a fost simplificată (redusă) la termenul unic de expresie din dreapta pentru a doua ecuație.
Simplificarea sau reducerea duce la un număr mai mic de porți pentru a implementa aceeași funcție ca un circuit. Un astfel de circuit mai mic poate face parte dintr-un circuit integrat (IC) sau poate fi un circuit autonom pe suprafața plăcii de bază a computerului.
Când o funcție (ecuație) ajunge la procesul de proiectare, trebuie să aibă loc simplificarea pentru a reduce numărul de porți și a ajunge la un circuit mai ieftin. Simplificarea necesită folosirea uneia sau mai multor din cele douăzeci și cinci de proprietăți booleene anterioare.
Exemplul 2.51:
Reduceți ecuația:
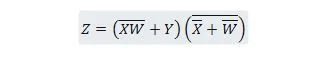
Notă: Două paranteze una lângă alta înseamnă că parantezele sunt marcate cu AND (punctul dintre ele nu a fost scris opțional).
Soluţie:
Pentru soluții, justificarea (motivul) pentru fiecare pas este dat în dreapta pasului, între paranteze. Cititorul ar trebui să citească fiecare pas și justificarea acestuia. Cititorul ar trebui să se refere și la proprietățile anterioare în timp ce citește pașii de reducere a funcției.
Exemplul 2.52:
Simplifica:
2.6 Suma minimă de produse
Următoarele două funcții sunt aceleași:
Se spune că ambele expresii din dreapta ambelor ecuații sunt sub forma Sumei Produselor (SP). Se spune că o expresie expresă este în forma Sumă produsului dacă nu are paranteze. Este evident că prima funcție (ecuația) are nevoie de mai multe porți decât a doua funcție.
Prima expresie din dreapta poate fi redusă pentru a obține a doua funcție. Cea de-a doua expresie din partea dreaptă nu poate fi simplificată în continuare și totuși poate fi exprimată ca Sumă de Produse („adăugarea” termenilor). A doua expresie din partea dreaptă nu poate fi simplificată mai mult. Deci, se spune că este în forma Sumei minime de produse (MSP).
Exemplul 2.61:
Aduceți următoarea funcție mai întâi în formularul Suma de produse și apoi în formularul Suma minimă de produse.
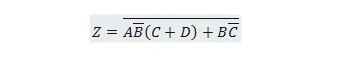
Soluţie:
Când se rezolvă probleme ca aceasta, una sau mai multe dintre cele douăzeci și cinci de proprietăți anterioare trebuie utilizate așa cum este ilustrat în această soluție:
2.6 Suma minimă de produse
Următoarele două funcții sunt aceleași:
Se spune că ambele expresii din dreapta ambelor ecuații sunt sub forma Sumei Produselor (SP). Se spune că o expresie expresă este în forma Sumă produsului dacă nu are paranteze. Este evident că prima funcție (ecuația) are nevoie de mai multe porți decât a doua funcție.
Prima expresie din dreapta poate fi redusă pentru a obține a doua funcție. Cea de-a doua expresie din partea dreaptă nu poate fi simplificată în continuare și totuși poate fi exprimată ca Sumă de Produse („adăugarea” termenilor). A doua expresie din partea dreaptă nu poate fi simplificată mai mult. Deci, se spune că este în forma Sumei minime de produse (MSP).
Exemplul 2.61:
Aduceți următoarea funcție mai întâi în formularul Suma de produse și apoi în formularul Suma minimă de produse.
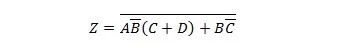
Soluţie:
Când rezolvați probleme de genul acesta, una sau mai multe dintre cele douăzeci și cinci de proprietăți anterioare trebuie utilizate așa cum este ilustrat în această soluție:
Această ultimă expresie este în forma Sumă de produse (SP), dar nu în forma Sumă minimă de produse (MSP). S-a răspuns la prima parte a întrebării. Soluția pentru a doua parte este următoarea:
Această ultimă funcție simplificată (ecuație) este în formă MSP și necesită un număr mai mic de porți pentru implementare decât forma SP corespunzătoare. Rețineți: SP înseamnă Suma de Produse, în timp ce MSP înseamnă Suma Minimă de Produse.
Exemplul 2.62:
Următorul circuit are intrările X, Y și W și Z este ieșirea. Produceți funcția Suma produselor (SP) (funcția Sumă minimă aparentă a produselor) pentru Z. Apoi, produceți Suma produselor (MSP) adevărată mai redusă (minimizat). Apoi, implementați circuitul MSP (desenați rețeaua de porți MSP).
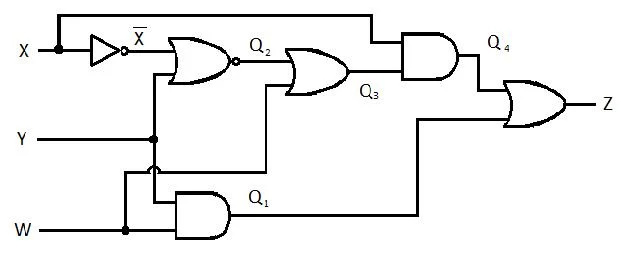
Fig 2.61 Un circuit de deschidere
Soluţie:
Înainte de a începe procesul de simplificare, expresia pentru Z trebuie obținută în termeni de X, Y și W. Consultați acest exemplu de ilustrare din diagramă:
Aceasta este expresia lui Z în termeni de X, Y și W. După aceasta, poate avea loc simplificarea la MSP aparent. MSP aparent este SP.
Această ultimă ecuație (funcție) este în formă SP. Nu este adevărată Suma Minimă de Produse (nu încă MSP). Deci, reducerea (minimizarea) trebuie să continue.
Această ultimă ecuație (funcție) este o adevărată Sumă Minimă de Produse (MSP). Și suma minimă de produse (minimizare adevărată) circuit de deschidere este:
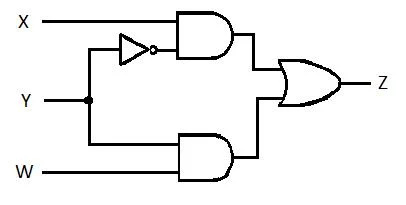
Fig 2.62 Circuitul MSP Gate
cometariu
Din analiza din această secțiune, se poate observa că nu este clar dacă Suma Produselor este Suma Minimă de Produse sau nu. SP nu este foarte util. Este MSP care este foarte util. Există o modalitate sigură de a obține MSP; este să folosești Harta Karnaugh. Harta Karnaugh depășește scopul acestui curs de carieră online.
2.7 Probleme
Cititorul este sfătuit să rezolve toate problemele dintr-un capitol înainte de a trece la capitolul următor.
- Produceți tabelele de adevăr ȘI, SAU și NU cu porțile corespunzătoare.
- Notează cele zece postulate booleene în diferitele lor categorii, denumind categoriile.
- Fără explicații, notează cele douăzeci și șase de proprietăți ale algebrei booleene în diferitele lor categorii, denumind categoriile.
- Reduceți ecuația folosind proprietățile booleene și citând categoriile utilizate.
- Reduceți ecuația folosind proprietățile booleene și citând categoriile utilizate.
- Folosind proprietățile booleene și citând categoriile utilizate, reduceți următoarea ecuație – mai întâi la Suma produselor și apoi la Suma minimă a produselor:
- Folosind proprietățile booleene și citând categoriile utilizate, reduceți următoarea ecuație – mai întâi la Suma produselor și apoi la Suma minimă a produselor:
